Anchor Box

Anchor boxex是学习卷积神经网络用于目标识别过程中最重要且最难理解的一个概念。这个概念最初是在Faster R-CNN中提出，之后在诸多优秀的目标识别中得到验证，本文主要参考自锚框: Anchor box综述

为什么需要anchor box？

先前的目标检测方式主要包括滑动窗口法和区域建议法，滑动窗口法存在窗口尺寸固定，窗口较多，运算量很大的问题；而区域建议法则是R-CNN的核心思想。通过CNN和RPN生成。通过RPN，生成候选区，然后输入到分类网络中得到最终的分类。

Anchor box

因为一个窗口只能检测一个目标，而且难以解决多尺度的问题，所以第二代检测中提出了特征金字塔的方法，对窗口进行不同分辨率尺度下的检测，但是这大大增加了计算量。

如图，红框中的人和车的中心点都在这个框中，然而按照以前的方法，一个格子能预测一个对象，而且他对于y输出的向量$y=[p_c, b_x, b_y, b_h, b_w, c_1, c_2]^T$，可以检测这三个类别，但是只能二选一，而不能都输出。所以回丢弃一种可能，导致一些对象无法被检测出来。因此引入了anchor box

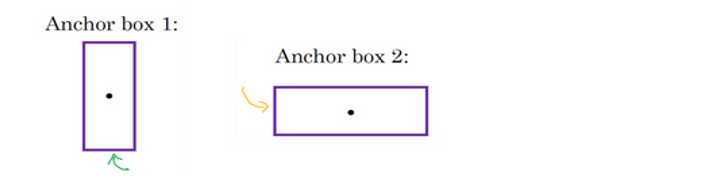
所以将上述张量重复两次，得到$y=[p_c, b_x, b_y, b_h, b_w, c_1, c_2, p_c, b_x, b_y, b_h, b_w, c_1, c_2]$。行人一般符合AB1的形状，而汽车符合AB2的形状，所以金标准应该是$y=[1, b_x, b_y, b_h, b_w, 1, 0, 1, b_x, b_y, b_h, b_2, 0, 1]$

为什么使用不同尺寸和不同的长宽比

为了得到较大的交并比
因为不同物体的形状是不一样的，车子的形状和人的形状应该使用不同长宽比的anchor box，从而提高IOU，那么如何选择anchor box的尺寸呢

人为经验选取
k-means聚类
作为超参数学习

Anchor box在各个阶段的使用

标注阶段

在训练阶段，是把anchor box作为训练样本，为了训练样本我们需要为每个锚框标注两类标签：一是锚框所含目标的类别，简称类别；二是真实边界框相对锚框的偏移量，简称偏移量（offset）
在目标检测时，我们首先生成多个锚框，然后为每个锚框预测类别以及偏移量，接着根据预测的偏移量调整锚框位置从而得到预测边界框，最后筛选需要输出的预测边界框。

假设图像中有$n_a$个anchor box，有$n_b$个真实边界框，那么就形成了一个anchor box与真实边界框之间的关系矩阵（一一对应关系）$X \in R^{n_a\times n_b}$，根据这个对应关系找出每个anchor box交并比最大的真实边框，然后以真实边框作为anchor box的边框，计算anchor box相对于真实边框的偏移量，如此就标记好了每个anchor box的标签和偏移量（这意味预测得到的anchor box永远无法实现标注的物体边框，而是只能尽量接近标注的物体边框，因为它的金标准也只是anchor box）

训练

在经过卷积和池化之后，在feature map层使用anchor box，经过一系列的特征提取，最后针对$3\times 3$网格会得到一个$3\times3\times2\times8$的特征层，其中2是anchor box的个数，用了2个anchor box， 8代表每个anchor box的8维特征向量，分别是4个位置偏移量（$H, W, X, Y$）和3个类别（one-hot），1个anchor box标注（anchor box与真实边框交并比最大则为1，否则为0）

前向传递得到anchor box之后，找到预先标注的anchor box，然后计算这个anchor box和ground truth之间的损失，训练的主要目的就是训练出用anchor box去拟合真实边框的模型参数.

损失函数（Faster R-CNN）

$L(\{p_i\}, \{t_i\}) =\frac{1}{N_{cls}}\sum_iL_{cls}(p_i, p_i^{*})+\lambda\frac{1}{N_{reg}}\sum_ip_i^*L_{reg}(t_i,t_i^*)$

$L{cls}(p_i, p_i^*)$代表类别损失，$L{reg}(t_i, t_i^*)$代表位置损失，$t_i^*$是真实的边框相对于anchor box4个参数化坐标的向量。

预测阶段

图像通过前向传递，最终生成多个anchor box，然后根据训练好的模型参数去预测这些anchor box的偏移量和类别，进而得到预测的边框值，由于阈值和anchor box数量选择问题，同一个目标可能会输出多个相似的预测边框，这样不仅不简洁，而且会增加计算量，为了解决这个问题，常常采用非极大值抑制。

我们常用IOU来代表置信度，什么意思呢？如下图，左图中存在三个框，计算这三个框之间的IOU，得出置信度得分。

流程如下

根据置信度得分进行排序
选择置信度最高的边框添加到最终输出列表中，将其从边框列表中删除
计算所有边界框的IoU
删除IoU大于阈值的边界框
重复上述过程，直到边界列表为空

def nms(bounding_boxes, confidence_score, threshold):
    # If no bounding boxes, return empty list
    if len(bounding_boxes) == 0:
        return [], []

    # Bounding boxes
    boxes = np.array(bounding_boxes)

    # coordinates of bounding boxes
    start_x = boxes[:, 0]
    start_y = boxes[:, 1]
    end_x = boxes[:, 2]
    end_y = boxes[:, 3]

    # Confidence scores of bounding boxes
    score = np.array(confidence_score)

    # Picked bounding boxes
    picked_boxes = []
    picked_score = []

    # Compute areas of bounding boxes
    areas = (end_x - start_x + 1) * (end_y - start_y + 1)

    # Sort by confidence score of bounding boxes
    order = np.argsort(score)

    # Iterate bounding boxes
    while order.size > 0:
        # The index of largest confidence score
        index = order[-1]

        # Pick the bounding box with largest confidence score
        picked_boxes.append(bounding_boxes[index])
        picked_score.append(confidence_score[index])

        # Compute ordinates of intersection-over-union(IOU)
        x1 = np.maximum(start_x[index], start_x[order[:-1]])
        x2 = np.minimum(end_x[index], end_x[order[:-1]])
        y1 = np.maximum(start_y[index], start_y[order[:-1]])
        y2 = np.minimum(end_y[index], end_y[order[:-1]])

        # Compute areas of intersection-over-union
        w = np.maximum(0.0, x2 - x1 + 1)
        h = np.maximum(0.0, y2 - y1 + 1)
        intersection = w * h

        # Compute the ratio between intersection and union
        ratio = intersection / (areas[index] + areas[order[:-1]] - intersection)

        left = np.where(ratio < threshold)
        order = order[left]

    return picked_boxes, picked_score